美国数学竞赛AMC简介，适合5年级及以上学生

AMC 全称是 American Mathematics Competitions，即美国数学竞赛。AMC 的前身为美国中学数学考试 American High School Mathematics Examination（AHSME），是美国数学协会 MAA（Mathematics Association of America）管理下的最热门，历史最悠久的学术比赛之一。

1950 年，第一届 AMC 数学竞赛在纽约举行，它当时仅提供给纽约地区的大约 200 所学校的近 6,000 名学生。 如今，该竞赛已发展涉及 4,000 多所学校，每年有超过 30 万名学生参加。它是面向全球中学生的国际性数学竞赛，也当之无愧是世界上目前最热门的中学生数学竞赛。

美国数学协会开展 AMC 数学竞赛的目的是加强美国年轻学子们对数学问题的解决能力。 通过课堂资源和友好竞争，MAA AMC 计划希望能够帮助美国的教育工作者发现人才并培养他们对数学的热爱，对创新社会中未来职业所需的分析技能产生积极影响。

这个竞赛还为美国培育世界数学奥林匹克（IMO）的国家队选手。通过 AMC 8、AMC 10、AMC 12、AIME 一系列 成熟的竞赛机制，AMC 的研究人员会从中找出绩优生参加美国数学奥林匹克（USAMO），再从中筛选出 24 至 30 位精英，参加暑期在大学举办的数学奥林匹克夏令营（MOSP）。再在夏令营中通过测试从其中选出六名队员代表美国参加世界数学奥林匹克比赛（IMO）。

为什么参加 AMC 数学竞赛?

众所周知，世界一流大学的本科入学竞争异常激烈，标准化考试高分和在校成绩拔尖是大学招生时的必备项；但仅凭这两点还不能说明学生在深入思考、探索和研究方面的能力。

所以很多中、美、加的优秀学生在做到上述两项之余，会投入相当的精力在 AP / IB / SATII、高含金量学科竞赛和科研项目几个方向，力求取得领先于大部分同龄人的成就，从而证明学校成绩和标化考试无法反映的深入理解和研究前沿学术问题的潜力。

在上图所示的学术金字塔中，在最具竞争力的塔顶端，除了科研项目之外，竞赛类成绩对于学生申请美国本科有举足轻重的作用，尤其是颇具影响力的美国数学竞赛（AMC）是美国大学申请最有价值的竞赛和活动之一。AMC 的成绩在选拔学生的过程中会扮演重要的角色。根据主流的申请网站和大学信息，MIT 、斯坦福、布朗等顶级大学已经把数学竞赛成绩排在了非常重要的参考因素之一。

从非学术的角度来讲，学习数学竞赛能开拓学生思维，把学过的一个概念应用于更综合、更深奥的问题中，培养深度思考的能力。遇到难题不畏惧，遇到简单题不骄躁，通过理智的分析，逐步解除复杂问题。这种解决问题的行为模式，能跳出学术的范畴，灵活应用到生活中，帮助学生取得成功。

AMC 竞赛的权威性

1. 目前世界上可信度最高的数学测试
2. 哈佛、麻省理工、普林斯顿三所顶级院校专家联合出题
3. 美国数学竞赛委员会颁发获奖证书
4. 每年超 30 万考生报名
5. 成绩优异者将受邀参加更高级比赛

AMC 竞赛的级别与难度

AMC 竞赛分为4个级别，分别是：AMC8、AMC10、AMC12、AIME 四个等级。

AMC8

针对 8 年级及以下的初中生或更低年级的学生。考试题型与美国 7，8 年级数学考试大纲相对应，其测验目的是为了增进学生对数学习题解答的能力。

就难度而言 AMC8 比较基础，题目范围由易至难，还涵盖了较广泛的数学实际应用。AMC8 获得高分的学生，可在学校允许后，受邀参加 AMC10 的比赛。

AMC10

针对 10 年级及以下 8 年级以上的学生（部分 AMC8 的优秀学生也可以参加）。其中成绩为 AMC10 竞赛参加者的前 2.5%，可受邀参加美国数学邀请赛（AIME）。

AMC10 主要目的是在刺激学生对数学的兴趣并且透过以选择题方式来开发学生对数学的才能，且测验的题型虽有一些挑战性，但是都不会超过学生的学习范围，题型范围由易到难。从 2020 年开始分为 A 赛和 B 赛，参赛者可以任意选择其中一项参加。

AMC12

针对12年级及以下的学生（对应国内高一、高二、高三的学生）。其中成绩为 AMC12 竞赛参加者的前 5% 的，可受邀参加美国数学邀请赛（AIME）。

AMC12 难度较高，其主要目的是刺激学生对数学的兴趣并且透过选择题的方式来开启学生对数学的才能。题目范围由易至难。从 2020 年开始分为A赛和B赛，参赛者可以任意选择其中一项参加。

AIME 

由 AMC10 的前 2.5% 和 AMC12 的前 5% 的参赛选手参加。是低于美国数学奥林匹克竞赛（USAMO）的一个数学竞赛，最主要的目的就是为美国奥数队选拔选手，优胜者会通过暑期集训筛选出最终的 6 位奥数国家队成员。

与 AMC10 和 AMC12 相比，AIME 提供了更进一步的挑战及认可，是四个级别中难度最高的。通过 AIME，可以让美国地区以外，在数学方面有优秀才能的学生通过国际性的数学测验提升了对自己的肯定。AIME 成绩优异的美国籍学生或在美国的合法居住者将再被邀请参加国数学奥林匹克竞赛（USAMO）数学测验。

ACM8

• AMC8 竞赛一共 25 道选择题，考试时间 40 分钟，满分 25 分。答对得一分，不同于 AMC10 和AMC12，答错或不答并不扣分。

AMC8 知识点分布

• 基础代数：整数、有理数、无理数、实数、数轴和直角坐标系；多元一次方程、简单二次方程、简单不等式；简单数列；基本代数技巧。
• 基础几何：基础几何作图；平面欧氏几何，点、线、三角形、特殊四边形、圆；规则图形的周长和面积；基本平面几何技巧；规则立体几何图形。
• 基础数论：奇偶分析、整除的性质、最小公倍数和最大公约数、同余问题。
• 基础组合：韦恩图；排列、组合和概率入门；阶乘和二项式系数、杨辉三角形。

AMC8 例题

ACM10

• AMC10 竞赛一共 25 道选择题，考试时间 75 分钟，满分 150 分，答对得 6 分，答错不得分，不答对 1.5分，2016 年起，AMC10 不再允许使用计算器
• AMC10 在每年11月举办

AMC10 知识点分布

• 进阶代数：多项式，余数定理，韦达定理，根与系数的关系，特殊高次方程；进阶不等式、均值不等式；函数入门，定义域和值域、二次函数、指数函数、对数函数、简单三角函数；数列进阶；代数技巧进阶。
• 进阶几何：进阶几何作图；三角形进阶、正弦定理、余弦定理、内切圆和外切圆、斯图瓦尔特定理、共点和共线；圆和四边形，四点共圆，圆的外切四边形；正多边形，角度，周长和面积；进阶平面几何技巧；解析几何入门。
• 立体几何：点、线、面的关系，三维坐标系；立体几何作图；正多面体，欧拉公式；特殊的立体几何图形，立体几何技巧。
• 进阶数论：数，数组和序列；模运算，复杂同余问题；整数、分数和小数，进制转换；基本丢番图方程，进阶数论技巧。
• 进阶组合：容斥原理；二项式定理及相关结论；进阶排列、组合和概率；期望入门，递推、二分法，进阶组合方法。

AMC10 例题

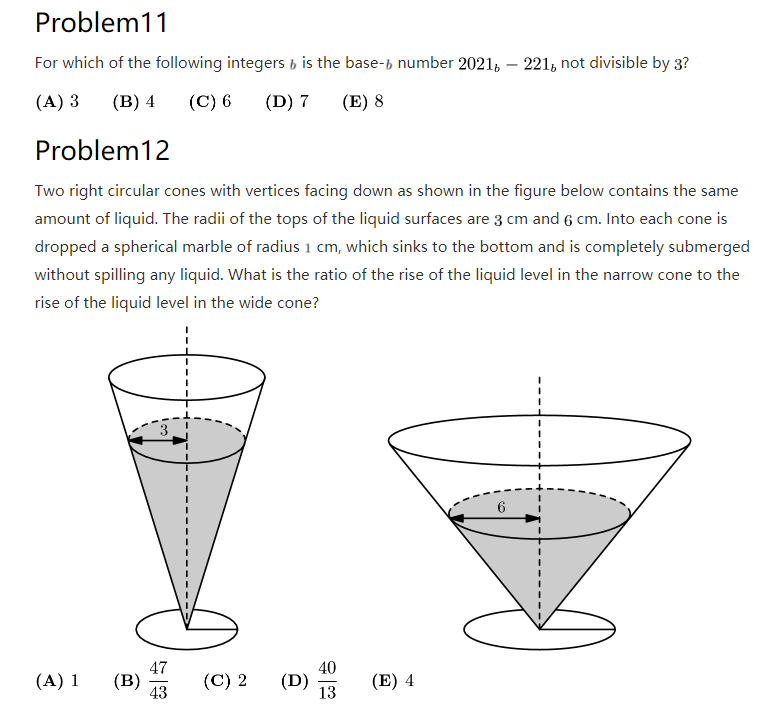
ACM12

• AMC12 竞赛一共 25 道选择题，考试时间 75 分钟，满分 150 分，答对得 6 分，答错不得分，不答对 1.5分，
• AMC12 通常在每年 11 月举办

AMC12 知识点分布

在 AMC10 基础上新增：

• 进阶代数：复杂不等式、调和不等式、轮换不等式、柯西不等式；复杂函数问题，反函数和符合函数，三角函数和差化积、积化和差，万能公式；复数，复平面，欧拉公式，蒂莫夫公式；数学归纳法、复杂数列和极限。
• 进阶几何：圆相关几何进阶；数形结合，二维、三维图形的函数表达，进阶解析几何；不规则二维、三维图形的处理；二维向量，三维向量。
• 进阶数论：二次余数，高次余数、费马圣诞节定理、费马小定理；各类丢番图方程的解法。
• 进阶组合：随机过程和期望。复杂组合问题技巧。
• 基本综合问题。

AIME

• AIME竞赛考试时间3小时，一共15题，均为应用题，满分15分，一题一分，答错不扣分。不允许使用计算器，前几道题为AMC12水平难度，最后的难度会相当有挑战性。
• AIME通常在每年三月下旬举办。

AIME 知识点分布

• 高阶代数：不等式专题、综合函数问题和复数专题、数列和极限专题。
• 高阶几何：圆专题、射影几何专题；解析几何专题，立体几何专题。
• 高阶数论：模运算专题；丢番图方程专题。
• 高阶组合：组合中的方法论专题。
• 进阶综合问题。

AIME 例题

来源网站：爱学